Question

Graph a line that is perpendicular to the given line. Determine the slope of the given line and the one you graphed in simplest form

Answer 1

Let's first identify at least two points that pass through the given line.

Let's use the following points:

Point A: x1, y1 = 0, -7

Point B: x2, y2 = 6, 2

a.) Let's determine the slope of the original line:

`\text{ m = }(y_2-y_1)/(x_2-x_1)`
`\text{ = }\frac{2\text{ - (-7)}}{6\text{ - 0}}\text{ = }\frac{2\text{ + 7}}{6}`
`\text{ m = }(9)/(6)\text{ = }((9)/(3))/((6)/(3))\text{ = }(3)/(2)`

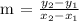
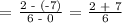
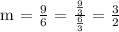
Therefore, the slope of the given line is 3/2.

b.) Let's determine the slope of the line perpendicular to the given line:

`\text{ m}_(\perp)\text{ = -}\frac{1}{\text{ m}}\text{ }`
`\text{ = -}(1)/((3)/(2))\text{ = -1 x }(2)/(3)`
`\text{ m}_(\perp)\text{ = -}(2)/(3)`

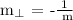
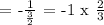
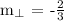
Therefore, the slope of the line perpendicular to the given line is -2/3.

c.) Let's plot the graph of the perpendicular line.

Let's first determine the equation of the given line.

m = 3/2

x,y = 0, -7

y = mx + b

-7 = (3/2)(0) + b

-7 = b

y = mx + b

y = 3/2x - 7

Let's determine the equation of the perpendicular line.

m = -2/3

x,y = 0, -7 ; let's use this as the point of intersection.

y = mx + b

-7 = -2/3(0) + b

-7 = b

y = mx + b

y = -2/3x - 7

Let's now plot the graph.