Let's first identify at least two points that pass through the given line.
Let's use the following points:
Point A: x1, y1 = 0, -7
Point B: x2, y2 = 6, 2
a.) Let's determine the slope of the original line:
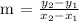
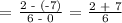
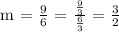
Therefore, the slope of the given line is 3/2.
b.) Let's determine the slope of the line perpendicular to the given line:
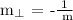


Therefore, the slope of the line perpendicular to the given line is -2/3.
c.) Let's plot the graph of the perpendicular line.
Let's first determine the equation of the given line.
m = 3/2
x,y = 0, -7
y = mx + b
-7 = (3/2)(0) + b
-7 = b
y = mx + b
y = 3/2x - 7
Let's determine the equation of the perpendicular line.
m = -2/3
x,y = 0, -7 ; let's use this as the point of intersection.
y = mx + b
-7 = -2/3(0) + b
-7 = b
y = mx + b
y = -2/3x - 7
Let's now plot the graph.