To find the initial population, we evaluate
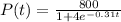
at t=0:
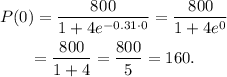
Therefore, the initial population was 160 individuals.
To find the population after 10 years, we evaluate the given function at t=10:
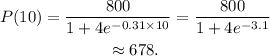
Therefore, the population after 10 years is 678 individuals.
Answer:
The initial population was 160 individuals.
The population after 10 years is 678 individuals.