Question

Integral 3/x^5 dx over (0,1]

Answer 1

Answer: We have to solve the following definite integral over a specified interval:

`\int_0^1(3)/(x^5)dx`

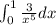
The solution steps are as follows:

`\begin{gathered} \int_0^1(3)/(x^5)dx=3\int_0^1(1)/(x^5)dx\Rightarrow(1) \\ \\ \end{gathered}`

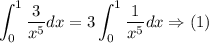
Applying the reverse power rule on the (1) gives the following answer:

`\begin{gathered} 3\int_0^1(1)/(x^5)dx=3[\int_0^1(1)/(x^5)dx=-(1)/(4x^4)] \\ \\ \\ \int_0^1(3)/(x^5)dx=[-(1)/(4x^4)]\rightarrow\text{ Evaluated at \lparen0,1\rparen} \\ \\ ----------------------- \\ -(1)/(4x^4)\rightarrow-(1)/(4(1)^4)-(-(1)/(4(0)^4)) \\ \\ \text{ Do note!} \\ (-(1)/(4(0)^4))\rightarrow\text{ Become infiniate} \\ \\ \text{ Therefore.} \\ \\ \\ -(1)/(4(1)^4)-(-(1)/(4(0)^4))=\text{ Diverges.} \\ \\ \text{ So the answer is:} \\ \\ \int_0^1(3)/(x^5)dx=\text{ Diverges} \end{gathered}`

The integral therefore diverges.

The plot of the parent function clearly shows the behavior between (0,1)