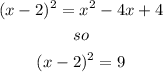Question

Which of the following is equivalent to 0 = 3x2 – 12x – 15 when completing the square?

Answer 1

The first thing we can do is notice that all the factors are divisible by 3. So we can divide both sides by 3 to get:

`\begin{gathered} (3x^2-12x-15)/(3)=(0)/(3) \\ (3x^2)/(3)-(12x)/(3)-(15)/(3)=0 \\ x^2-4x-5=0 \end{gathered}`

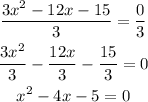
A square can be written in this way:

`(x-a)^2=x^2-2ax+a^2`

Comparing it to our equation, we see the x² is already equal. Comparing the second term, we get:

`\begin{gathered} -4=-2a \\ -2a=-4 \\ a=(-4)/(-2) \\ a=2 \end{gathered}`

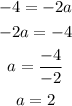
So, if a = 2, then a² = 4. However, we have -5 instead of 4. To fix this, we can add 9 to both sides:

`\begin{gathered} x^2-4x-5+9=0+9 \\ x^2-4x+4=9 \end{gathered}`

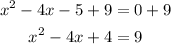
And now we have the right square:

`\begin{gathered} (x-2)^2=x^2-4x+4 \\ so \\ (x-2)^2=9 \end{gathered}`