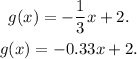Question

Type an equation for the line described. Type your answer in the form g(x)=mx+b. If a value is not an integer type it as a decimal rounded to the nearest hundredth.

Answer 1

Recall that two lines are perpendicular if the product of their slopes is equal to -1.

Notice that f(x) is given in slope-intercept form, then, the slope of f(x) is 3. Therefore, the slope of g(x) must be

`-(1)/(3)\text{.}`

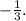
Now, to determine the equation of g(x) we will use the following formula:

`y(x)-y_0=m(x-x_0),`

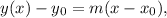
where (x₀,y₀) is a point on the line, and m is the slope.

Substituting m=-1/3 and (x₀,y₀)=(3,1), we get:

`g(x)-1=-(1)/(3)(x-3)\text{.}`

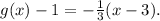
Taking the above equation to its slope-intercept form we get:

`g(x)=-(1)/(3)x+2.`

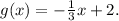
Answer:

Slope:

`-(1)/(3)=-0.33\text{.}`

Equation:

`\begin{gathered} g(x)=-(1)/(3)x+2. \\ g(x)=-0.33x+2. \end{gathered}`