Note that in composite functions :
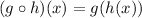
g of h of x can be written in the expression above.
From the problem,
g(t) = t + 5
h(t) = 3t - 2
Find (g o h)(-4 + t)
First step is to evaluate h(-4 + t) using the function h in the given :
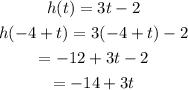
Next step is to evaluate g(-14 + 3t) which is the result in function h.
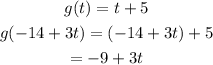
Therefore, the answer is -9 + 3t or 3t - 9