Question

I’m not sure how to do this or what the answer is

Answer 1

Note that in composite functions :

`(g\circ h)(x)=g(h(x))`

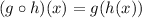
g of h of x can be written in the expression above.

From the problem,

g(t) = t + 5

h(t) = 3t - 2

Find (g o h)(-4 + t)

First step is to evaluate h(-4 + t) using the function h in the given :

`\begin{gathered} h(t)=3t-2 \\ h(-4+t)=3(-4+t)-2 \\ =-12+3t-2 \\ =-14+3t \end{gathered}`

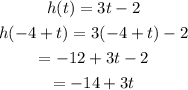
Next step is to evaluate g(-14 + 3t) which is the result in function h.

`\begin{gathered} g(t)=t+5 \\ g(-14+3t)=(-14+3t)+5 \\ =-9+3t \end{gathered}`

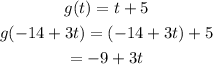
Therefore, the answer is -9 + 3t or 3t - 9