Assume X(3,2) and Y(6,8).
Let Z be the point which is 3/5 of the way between XY. So,
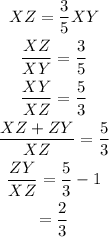
So point Z divide the line XY in ratio 3:2.
The coordinate of point P if it divide the line A(x_1,y_1) and B(x_2,y_2) in ratio m:n is,

Determine the coordinate of point the divide the line joining points (3,2) and (6,8) in 3:2 ratio.
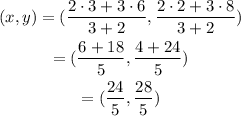
So value of coodinate is (24/5,28/5)