Question

Please help !Find a.Round to the nearest tenth:27 cm10228a = [? ]cmLaw of Sines: sin Asin Csin BbaA=?

Answer 1

Use the Law of Sines to find a:

`(a)/(\sin(A))=(27cm)/(\sin (28º))`

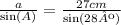
Since both a and the angle A are unkowns, we need to find the measure of the angle opposite to the side A first. Notice that two of the interior angles of the triangle are given. Remember that the sum of the internal angles of every triangle must add up to 180º.

Then:

`\begin{gathered} A+102+28=180 \\ \Rightarrow A+130=180 \\ \Rightarrow A=180-130 \\ \therefore A=50 \end{gathered}`

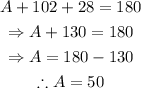
Then, the angle opposite to the side with length a has a measure of 50º.

Isolate a from the equation of the law of sines and replace A=50º to find the length a:

`\begin{gathered} \Rightarrow a=(\sin(A))/(\sin(28º))*27cm \\ =(\sin(50º))/(\sin(28º))*27cm \\ =44.0563425\ldots cm \\ \approx44.1cm \end{gathered}`

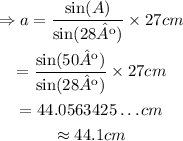
Therefore, to the nearest tenth, the length of a is equal to 44.1cm.