The given equation is already balanced. We can use the stoichiometric ratio given by the equation to find how many moles of KNO3 are produced. According to the equation, for every mole of Pb(NO3)2, 2 moles of KNO3 are produced.
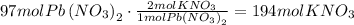
It means that 194moles of KNO3 are produced.