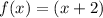
Step-by-step explanation
Step 1
Let
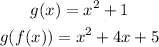
so,
A composite function is generally a function that is written inside another function. Composition of a function is done by substituting one function into another function
so, when evaluate f(x) into g(x) we got
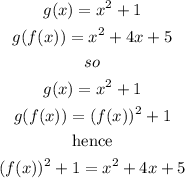
Step 2
solve for f(x)
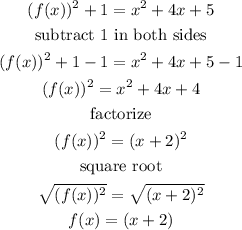
therefore, the answer is
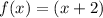
I hope this helps you