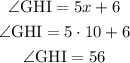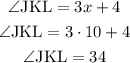The angles ∠GHI and ∠JKL are complementary, this means that they add up to 90°
Then we can say that
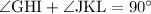
For
∠GHI= (5x+6)°
∠JKL= (3x+4)°
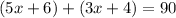
From this expression you can calculate the value of x
First step is to order the like terms together and simplify them}
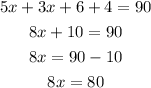
Next divide both sides of the equation by 8 to reach the value of x
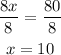
Now that we knoe the value of x, we can calculate the measure of both angles