Question

!) f(x + 2) f(x + bx) Sketching a Graph of a Function In Exercises 31–38, sketch a graph of the function and find its domain and range, Use a graphing utility to verify your graph. 31.) S(x) = 4 - x

Answer 1

31.

The domain of a function is the set of all values that its variable can take.

To find the domain of a function, search for restrictions over its variable in its rule of correspondence. Remember that common restrictions are:

1. The denominator must be different to 0.

2. The argument of square roots cannot be negative.

For the given function:

`f(x)=4-x`

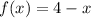
In this rule of correspondence, the variable x does not appear in a denominator or inside a square root. Then, there are no restrictions over the variable x and the domain is the set of all real numbers, which can be represented using interval notation as:

`(-\infty,\infty)`

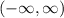
To sketch the graph of the function, notice that it is the equation of a line with slope -1 and y-intercept 4: