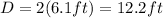Question

8. A yellow-pink spotlight was positioned directly above Usher during the Global Citizen's Concert. If the surface area of the cone of light was approximately 500 square feet and the slant height was 20 feet, find the diameter of lighton stage.

Answer 1

We are given the surface area of a cone and we are asked to find its diameter. To do that, let's remember the formula for the surface area of a cone:

`A=\pi r^2+\pi rl`

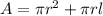
Where "r" is the radius, "h" is the height and "l" is the slant height. We are given the following values:

`\begin{gathered} A=500ft^2 \\ l=20ft \end{gathered}`

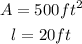
Replacing in the formula we get:

`500=\pi r^2+20\pi r`

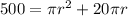
Now we need to solve for "r", to do that we will subtract 500 on both sides:

`\pi r^2+20\pi r-500=0`

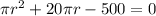
Now we will use the quadratic formula to find the values of "r". The quadratic formula is the following:

`r=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where:

`\begin{gathered} a=\pi \\ b=20\pi \\ c=-500 \end{gathered}`

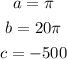
Replacing in the quadratic formula we get:

`r=\frac{-20\pi\pm\sqrt[]{400\pi^2-4(\pi)(-500)}}{2\pi}`

simplifying:

`r=\frac{-20\pi\pm\sqrt[]{400\pi^2+2000\pi}}{2\pi}`

Solving the operations inside the radical we get:

`r=(-20\pi\pm101.15)/(2\pi)`

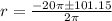
Now we take the positive sing and solve the operations, like this:

`r=(-20\pi+101.15)/(2\pi)=6.1`

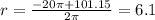
Taking the negative sing we get:

`r=(-20\pi-101.15)/(2\pi)=-26.1`

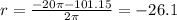
Since the radius should be a positive quantity we take the first value, therefore the radius is 6.1 ft. To get the diameter we use:

`D=2r`

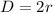
Therefore the diameter is:

`D=2(6.1ft)=12.2ft`