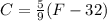We need to rewrite the equation
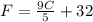
isolating C on the left side of the equation.
First, we can subtract 9C/5 from both sides of the equation. We obtain:
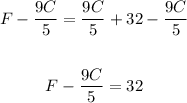
Then, we can subtract F from both sides of the equation. We obtain:
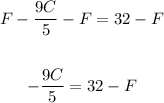
Then, we can multiply both sides by -5/9. We obtain:
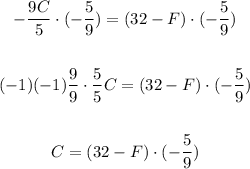
Then, we can distribute the factor -5/9 over the sum 32-F on the right side:
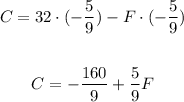
Therefore, the answer can be written as
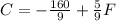
Or as