Given the expression:
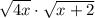
You need to apply the Property for Radicals that states that the Multiplication of two roots with the same indices is equal to the root of the Product. Then:
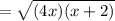
Apply the Distributive Property inside the square root:
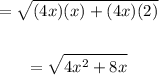
By definition, the Radicand (the value inside the square root) must be greater than or equal to zero:
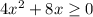
Solving for "x", you get:
- Case 1
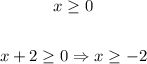
- Case 2:
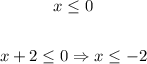
By determining the Intersection, you get that the solution is:
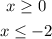
Hence, the answer is: Option B and Option D.