we write the sentences in mathematical expressions
(x is the value for each apples and y for each oranges)
Jimmy had bought 6 apples and 12 oranges for a total of $33.
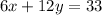
Emma had bought 20 apples and 15 oranges for the total of $60

now we try to solve the two equations
I will solve x from the first equation and replace on the second to find y
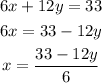
replacing and solving y
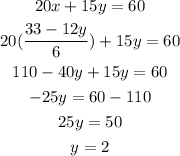
y=2 so, the cost of the orange is $2
now replace y=2 on any equation to find x
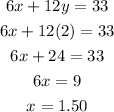
the cost of the apples is $1.50