Question

Which table of ordered pairs represents a proportional relationship? 31 Х 4 7 10 y 8 11 14 х 5 7 9 y 25 49 81 Х 6 10 14 у 3 5 7 3 8 13 у 6 11 18

Answer 1

A table that represents a proportional relationship will be the one in which every element in y is a constant multiple of the corresponding element in x.

In other words, the points of the table must lie on a line that must pass through the origin.

Let us check each of the tables one by one.

Table 1.

`(11-8)/(7-4)=1`

and

`(14-11)/(10-7)=1`

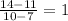
The difference between the two points is the same BUT every element in y is not a constant multiple of x; therefore, this choice is not correct.

But just to make sure, let us go through other remaining two tables.

`(49-25)/(7-5)=12`

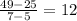
and

`(81-49)/(9-7)=16`

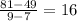
these two slope are not the same; therefore, this is not the right table.

Now for the third table.

`(5-3)/(10-6)=0.5`

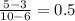
and

`(7-5)/(14-10)=0.5`

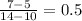
This table is the correct answer!

Let us now do table 4

`(11-6)/(8-3)=1`

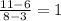
and

`(18-11)/(13-8)=(7)/(5)`

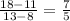
the two slopes are not equal; therefore, this table does not represent a proportional relationship.

Hence, the third table is the correct one.