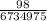Given:
• Top cash prize = $697
,
• First set of numbers to pick 4 different numbers from = 1 to 53
,
• Second set to pick one number from = 1 to 46
,
• Minimum award = $225
Given that the player wins the minimum award by matching three numbers drawn from 1 to 53 and matching number through 1 to 43, let's find the probability of winning the minimum award.
To find the probability, we have the following:
Number of ways to pick 4 different numbers from 1 to 53:

Now, the probability of matching 3 numbers from the 4 different numbers picked and matching the number on the gold ball (1 to 46) will be:

Therefore, the probability of winning a minimum award is:
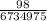
• ANSWER: