Given the points (-11, -12) and (-8,-21), you can calculate the slope of the line that passes through them using the following formula:
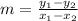
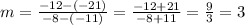
The slope is m=3
Now with one of the points and the slope you can determine the equation using the point slope form:

(-11,-12)
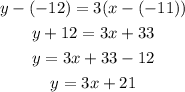
The y-intercept is the value of y when x=0, from the equation:
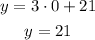
So,
The slope is 3
The y-intercept is 21
The equation is y=3x+21