Question

The revenue for a company producing widgets by y=-25x^2-35x+300, where x is the price dollars for each each widget. The cost for the production is given by y=25x-10. determine the price that will allow the production of widget to break even.

Answer 1

The price that will allow the production of widget to break even is $2.52

Step-by-step explanation:

Given the revenue of

`y=-25x^2-35x+300`

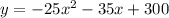
cost as

`y=25x-10`

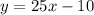
To obtain break even, we make the revenue equal to the cost.

That is:

`-25x^2-35x+300=25x-10`

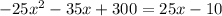
Now, we solve the equation

`\begin{gathered} -25x^2-35x-25x=-10-300 \\ \\ -25x^2-60x=-310 \\ \text{Divide both sides by -5} \\ 5x^2+12x=62 \\ \\ 5x^2+12x-62=0 \\ \end{gathered}`

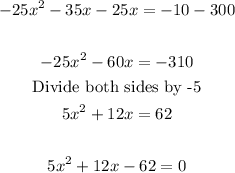
Using the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ \text{Here:} \\ a=5 \\ b=12 \\ c=-62 \\ \\ \\ x=\frac{-12\pm\sqrt[]{12^2-4(5)(-62})}{2(5)} \\ \\ =\frac{-12\pm\sqrt[]{144^{}+1240}}{10} \\ \\ =\frac{-12\pm\sqrt[]{1384}}{10} \\ \\ =(-12\pm37.2)/(10) \\ \\ x=2.52 \\ OR \\ x=-4.92 \end{gathered}`

The price that will allow the production of widget to break even is $2.52