Answer:
The price that will allow the production of widget to break even is $2.52
Step-by-step explanation:
Given the revenue of
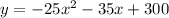
cost as
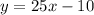
To obtain break even, we make the revenue equal to the cost.
That is:
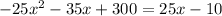
Now, we solve the equation
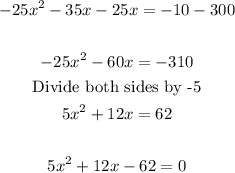
Using the quadratic formula:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ \text{Here:} \\ a=5 \\ b=12 \\ c=-62 \\ \\ \\ x=\frac{-12\pm\sqrt[]{12^2-4(5)(-62})}{2(5)} \\ \\ =\frac{-12\pm\sqrt[]{144^{}+1240}}{10} \\ \\ =\frac{-12\pm\sqrt[]{1384}}{10} \\ \\ =(-12\pm37.2)/(10) \\ \\ x=2.52 \\ OR \\ x=-4.92 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wi62lljdsxrawqdoret8328093cc4rgn4e.png)
The price that will allow the production of widget to break even is $2.52