Step 1
The property of a parallelogram is that diagonals of a parallelogram bisect each other and hence have the same midpoint.
This means that the diagonals cut themselves into two equal halves.
Hence, they must have the same mid-points.
Therefore, if we prove that AC and BD have the same midpoint, then ABCD is a parallelogram.
Step 2
Find the midpoint of BD and AC
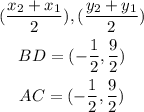
Since they have the same midpoint, the answer will be;
We Prove that AC and BD have the same midpoint which we have done. we know the diagonals of a parallelogram bisect each other; therefore, they have the same midpoint and ABCD is a parallelogram.