Question

Last year, Linda had $20,000 to invest. She invested some of it in an account that paid 7% simple interest per year, and she invested the rest in an account that paid 9% simple interest per year. After one year, she received a total of $1780 in interest. How much did she invest in each account?First account:Second account:Solve by tax rate or interest rate using system of linear equations.

Answer 1

First account: $1000

Second account: $19000

Step-by-step explanation

The formula to find the simple interest is,

`i=P\cdot r\cdot t`

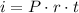
Where P is the principal amount, r is the interest rate as a decimal, and t is the time in years.

In this problem, the interest is calculated after 1 year, so t = 1.

Let x be the amount she invested in the account that paid 7% interest a year and y be the amount she invested in the account that paid 9% interest a year. We know that the sum of the two invested amounts is $20,000,

`x+y=20000`

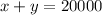
And we know that the total interest earned was $1780, which is,

`0.07x+0.09y=1780`

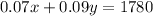
Here we have a system of linear equations for x and y. To solve it, we can use the method of elimination: first, multiply the first equation by 0.07,

`\begin{gathered} 0.07(x+y)=0.07\cdot20000 \\ 0.07x+0.07y=1400 \end{gathered}`

And subtract it from the second equation,

`\begin{gathered} (0.07x-0.07x)+(0.09y-0.07y)=1780-1400 \\ 0.02y=380 \end{gathered}`

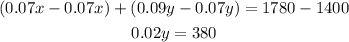
Then divide both sides by 0.02,

`\begin{gathered} (0.02y)/(0.02)=(380)/(0.02) \\ \\ y=19000 \end{gathered}`

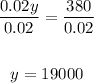
Now, use the first equation to find x,

`x=20000-y=20000-19000=1000`

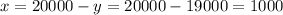
Hence, Linda invested $1000 in the first account and $19000 in the second account.