cosθ = -√15/4
STEP - BY - STEP EXPLANATION
What to find?
cos(θ )
Given:
sin(θ ) = −1/4
To solve the given problem, we will follow the steps below:
Step 1
Recall the trigonometric identities.
cos²θ + sin²θ = 1
Step 2
Substitute the value of sinθ into the above.
cos²θ + (-1/4)² = 1
cos²θ + 1/16 = 1
Step 3
Subtract 1/16 from both-side of the equation.
cos²θ = 1 - 1/16
Step 4
Simplify the right-hand side of the equation.
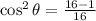
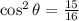
Step 5
Take the square root of both-side of the equation.
![\cos \theta=\pm\sqrt[]{(15)/(16)}](https://img.qammunity.org/2023/formulas/mathematics/college/6i4gpsmn8k0k6tnurkql3tvpt9r1161nwd.png)
![\cos \theta=\pm\frac{\sqrt[]{15}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/6jll2gntyumk1rwdzovcdcrw0mwbhyd0ec.png)
Since θ is in the third quadrant;
We can see that in the third quadrant, only tanθ is positive, cosθ is negative.
Hence, we will pick only the negative value.
Therefore,
![\cos \theta=\frac{-\text{ }\sqrt[]{15}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/9ihiko0j2ug1as80try5xybynrsy0qayqy.png)