Question

Solve the system graphically and check x+2y the solution.2x+5y=0. X+6y=14

Answer 1

Given:

The system of the equation is,

`\begin{gathered} 2x+5y=0 \\ x+6y=14 \end{gathered}`

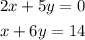
Draw the lines on the graph, the point at which the lines intersects. That point will be the solution of the system.

The points on the line 2x+5y=0 are,

`\begin{gathered} 2x+5y=0 \\ x=0\Rightarrow y=0 \\ x=5\Rightarrow y=-2 \\ x=-10\Rightarrow y=4 \end{gathered}`

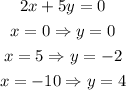
And the points on the line x+6y=14

`\begin{gathered} x+6y=14 \\ x=0\Rightarrow y=(7)/(3) \\ x=14\Rightarrow y=0 \\ x=-10\Rightarrow y=4 \end{gathered}`

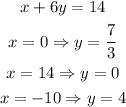
The graph of the lines is,

As the point of intersection is ( -10,4).

The solution of the given system of equation is x = -10, y = 4.