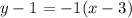Answer:
The equation of the line in slope intercept form is;
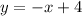
And the equation of the line in point-slope form is;
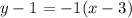
Step-by-step explanation:
We want to write a linear equation that passes through the points;
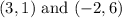
Firstly, let us find the slope of the line;
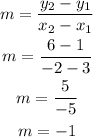
So, we can now use the point-slope equation of line to find the equation of the line;
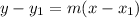
using the point given;
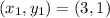
And the derived slope, we have;
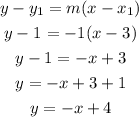
Therefore, the equation of the line in slope intercept form is;
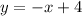
And the equation of the line in point-slope form is;