Question

The sum of the two digits of a number is equal to the triple of the tens digit. If we multiply this number by four and subtract fifty four of this product, the result is equal to the number obtained by allowing the digits of the original number. What is this number ?

Answer 1

Let n be the number we are looking for.

It has, at least, two digits + a tens digit which can be represented as ab.c where a, b, and c is a number from 1 to 9.

The first part of the problem can be written mathematically as:

`a+b=3c`

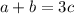
The second part of the sentence states that:

`\begin{gathered} 4n-54=cb.a \\ \Rightarrow n=(cba+54)/(4) \\ \Rightarrow ab\mathrm{}c=(cba+54)/(4)=(cba)/(4)+13.5 \end{gathered}`

From the first equation, c could be equal to 1, 2, 3, 4, 5, or 6 since a+b cannot be greater than 18 nor lesser than 0 (that would imply a=b=c=0).