Question

Find two positive numbers whose Difference is two and whose product is 1443

Answer 1

Step-by-step explanation

In the question, we are asked to find two positive numbers whose Difference is two and whose product is 1443.

If we let the numbers be x and y, therefore we can create the equation below,

`\begin{gathered} x-y=2\text{ ------(1)} \\ xy=1443-----(2) \end{gathered}`

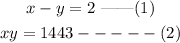
But;

`x=y+2----(3)`

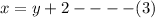
Substitute equation 3 in equation 2

`\begin{gathered} y(y+2)=1443 \\ y^2+2y=1443 \\ y^2+2y-1443=0 \end{gathered}`

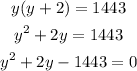
Using the quadratic formula;

`\begin{gathered} y=_{}\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where a =1, b=2 and c=-1443} \end{gathered}`

Therefore;

`\begin{gathered} y_(1,\: 2)=\frac{-2\pm\sqrt[]{2^2-4*\: 1*\mleft(-1443\mright)}}{2*\: 1} \\ y_(1,\: 2)=(-2\pm\: 76)/(2*\: 1) \\ y_1=(-2+76)/(2*1)=37 \\ y_2=(-2-76)/(2*\: 1)=-39 \end{gathered}`

Since we need only the positive value, we will substitute y=37 in equation three.

`\begin{gathered} x=37+2 \\ x=39 \end{gathered}`

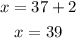
Answer: The two numbers are 37 and 39