Step-by-step explanation
In the question, we are asked to find two positive numbers whose Difference is two and whose product is 1443.
If we let the numbers be x and y, therefore we can create the equation below,
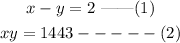
But;

Substitute equation 3 in equation 2
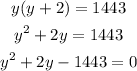
Using the quadratic formula;
![\begin{gathered} y=_{}\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where a =1, b=2 and c=-1443} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ekxc71qts7mnedv1une4oyfm14qi5nm5ex.png)
Therefore;
![\begin{gathered} y_(1,\: 2)=\frac{-2\pm\sqrt[]{2^2-4*\: 1*\mleft(-1443\mright)}}{2*\: 1} \\ y_(1,\: 2)=(-2\pm\: 76)/(2*\: 1) \\ y_1=(-2+76)/(2*1)=37 \\ y_2=(-2-76)/(2*\: 1)=-39 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/adhgvpevd29cxq84vepoqynrwpjrlnvqpt.png)
Since we need only the positive value, we will substitute y=37 in equation three.
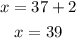
Answer: The two numbers are 37 and 39