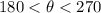Question

If sine < 0 and tane > 0 then: A. 270° < < 360° B. 180° < 9

Answer 1

So,

Given that:

`\begin{gathered} \sin (\theta)<0 \\ \tan (\theta)>0 \end{gathered}`

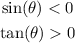
We could graph this situation here below:

The function sin(x) is negative in the third and fourth quadrant. And, the function tan(x) is positive in the one and third quadrant. As you can see, the quadrant that satisfies that sin(x) is negative and tan(x) is positive is the third, so our angle will be in that quadrant.

Now, the third quadrant comprises values ​​between pi and 3pi/2, (which in degrees is 180° and 270°). so we could affirm that:

`180<\theta<270`