Answer:
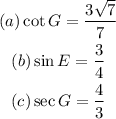
Explanation:
A sketch of the triangle and the given dimensions is attached below:
First, find the length of EF using the Pythagorean Theorem:
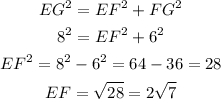
(a)cot G
Cotangent is the inverse of tangent.
• The side length opposite to G = 2√7
,
• The side length adjacent to G = 6

(b)sin E
• The side length ,opposite, to E = 6
,
• The length of the ,hypotenuse, = 8

(c)sec G
Secant is the inverse of cosine.
• The side length adjacent to G = 6
,
• The length of the hypotenuse = 8
