The derivative of the y function represents the slope of the function on each point. y is a function of x, if we differentiate our curve, we're going to have
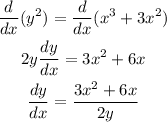
The derivative at x = -3 diverges(when x = -3, y = 0), therefore, we have a vertical asymptote.