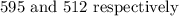Step 1
Given; 574, 526, 512, 579, 595, 517, 524, 552, 558, 541
Required; To create a box plot
Step 2
Arrange in ascending order
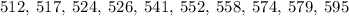
Find the lower quartile
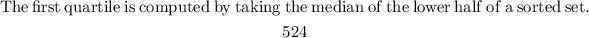
Find the upper quartile
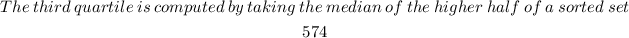
The median is the middle number of the entire data
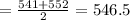
The maximum and minimum values are;