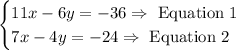
We can do the following steps to solve the system of equations using the elimination method.
Step 1: We multiply Equation 1 by 7 and the Equation 2 by -11.
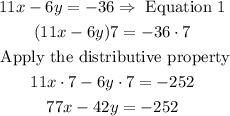
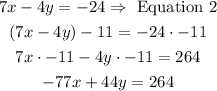
Step 2: We add the resulting equations.
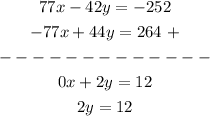
Step 3: We solve the above equation.
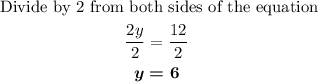
Step 4: We replace the obtained value in any initial equation. For example, in Equation 1.

Therefore, the solution of the system of equations is the ordered pair (0,6).