ANSWER
sec²θ + tan²θ = 1
Step-by-step explanation
The main Pythagorean identity is,

If we subtract sin²θ from both sides, we obtain the second option given,
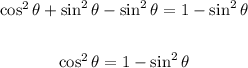
And, if we divide both sides by cos²θ, we obtain the third option given,
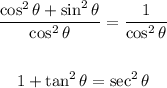
Hence, the last option, sec²θ + tan²θ = 1 is not a valid Pythagorean identity.