PART A:
The zeros of the function are the values of t where we have h = 0.
Looking at the table, the zeros are t = 0 and t = 10.5
PART B:
Let's write the function using the factored form of the quadratic equation:

Since the zeros are 0 and 10.5, we have t1 = 0 and t2 = 10.5, so:
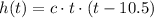
Now, using the point (2, 272) from the table, we have:
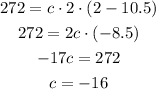
So our function is:
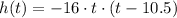
PART C:
First let's expand our function to the standard form:
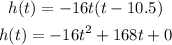
Comparing with the given model, we have V0 = 168 ft/s (because the coefficient multiplying the variable t is 168 in our function and V0 in the given model).
PART D:
First, let's calculate the average value between the zeros:
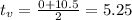
Using this value of t in the function, we have:
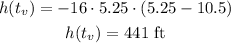
So the maximum height is 441 ft.