Question

The projected profit (in thousands of dollars) of a new technology company in year t can be modeled by the polynomial 2t2 - 9t - 18

When the company will break even (have zero profit)? Show all work necessary to justify your answer.
The projected profit (in thousands of dollars) in year t of a newly developed line of business can be modeled by the monomial t3 . Write a polynomial that models the company’s total profit including this new line of business.
How many years sooner will the company break even with the new line of business? Show all work necessary to justify your answer.

Answer 1

Answer:

a. The company will break even in 6 years

b. The total profit with the newly developed line of business is:

`t^3+2t^2-9t-18`

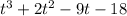
c. The company will break even 3 years sooner

Step-by-step explanation:

The projected profit is given as:

`2t^2-9t-18`

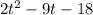
a. The company will break even when the profit is zero. That is;

`\begin{gathered} 2t^2-9t-18=0 \\ \\ (2t+3)(t-6)=0 \\ 2t+3=0 \\ \Rightarrow t=-(3)/(2) \\ \\ t-6=0 \\ t=6 \end{gathered}`

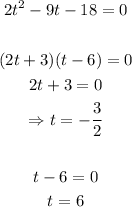
6 is the realistic number of years (As we cannot have -3/2 years).

We conclude that they will break even in 6 years

b. The projected profit of a newly developed line of business is:

`t^3`

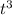
The total profit is now;

`t^3+2t^2-9t-18`

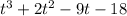
The company will break even with this new line of business as follows:

`\begin{gathered} t^3+2t^2-9t-18=0 \\ (t+2)(t+3)(t-3) \\ t+2=0 \\ \Rightarrow t=-2 \\ t+3=0 \\ \Rightarrow t=-3 \\ t-3=0 \\ \Rightarrow t=3 \end{gathered}`

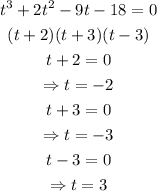
We choose t = 3 (because we cannot have -2 years or -3 years)

The difference between this and the previous time is 6 - 3 = 3 years

The company will break even 3 years sooner