Given:
The position of the small plane is given by,
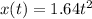
Step-by-step explanation:
The accelration of plane can be obtained by double derivative of the position function.
Determine the double derivative of the position function.
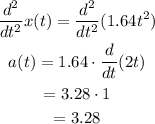
So acceleration of the small plane is 3.28 m/s^2
Answer: 3.28