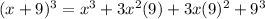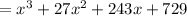Question

The formula V=4/3 pie r3 gives the volume with radius r. Find the volume of a sphere with radius x+9. Write your answer as standard form.

Answer 1

We will find it as follows:

`V=(4)/(3)\pi(x+9)^3\Rightarrow V=(4\pi)/(3)(x^3+27x^2+243x+729)^{}`
`\Rightarrow V=(4)/(3)\pi x^3+36\pi x^2+324x+972`

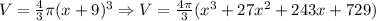
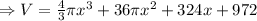
The volume of such a sphere is given by the expression found.

***

When we have a binomial at the power of a number, of the form:

`(a+b)^n`

We use Pascal's triangle to determine the expansion. Pascal's triangle is the following:

Each row can be used to calculate a specific power, in our case the binomial is at the power of three, and we will use the 4rth row to expand, that is:

`(a+b)^3=a^3+3a^2b+3ab^2+b^3`

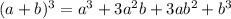
As you can see, the numbers that accompany a & b are the ones found in the 4th row of Pascal's triangle. We also see that the "degree" o the expansion always sums 3, that is a^3 has an overall degree of 3, a^2b has an overall degree of 3, ab^2 has an overall degree of 3 & b^3 has an overall degree of 3.

***

If we, for example, wanted to expand (a + b)^4, we then would have the following:

*We would use the 5th row and get:

`(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4`

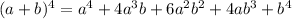
[Pascal's triangle expands to infinity. So, you in theory can manually expand any binomial at any power, but for big numbers, it will take a long time]

***

In our case, the binomial was:

`(x+9)^3`

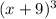
And, its respective expansion is:

`(x+9)^3=x^3+3x^2(9)+3x(9)^2+9^3`
`=x^3+27x^2+243x+729`