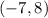Question

Can you help me find the scale factor and center of dilation and simplify the answer as a fraction or whole number please

Answer 1

To find the scale factor let's use the fact that

`k\cdot\overline{SU}=\overline{S'U'}`

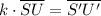
Therefore let's find SU and S'U' length

`\begin{gathered} \overline{SU}=\sqrt[]{4^2+8^2} \\ \\ \overline{SU}=\sqrt[]{80} \end{gathered}`

And S'U'

`\begin{gathered} \overline{S^(\prime)U^(\prime)}=\sqrt[]{2^2+4^2} \\ \\ \overline{S^(\prime)U^(\prime)}=\sqrt[]{20} \end{gathered}`

Using our first equation:

`\begin{gathered} k\cdot\overline{SU}=\overline{S^(\prime)U^(\prime)}\Rightarrow k=\frac{\overline{S^(\prime)U^(\prime)}}{\overline{SU}} \\ \\ k=\frac{\sqrt[]{20}}{\overline{\sqrt[]{80}}} \\ \\ k=\sqrt[]{(1)/(4)} \\ \\ k=(1)/(2) \end{gathered}`

And to find the center of dilatation we can use the equation:

`\begin{gathered} T=(x_1,y_1) \\ T^(\prime)=(x_2,y_2) \\ \\ x_0=(kx_1-x_2)/(k-1) \\ \\ y_0=(ky_1-y_2)/(k-1) \end{gathered}`

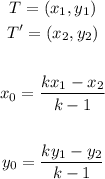
Where (x₀, y₀) is the center of dilatation, using the point T a reference we get

`\begin{gathered} T=(9_{},0) \\ T^(\prime)=(1_{},4) \\ \\ x_0=\frac{(1)/(2)\cdot9_{}-1}{(1)/(2)-1}=-7 \\ \\ y_0=((1)/(2)\cdot0-4)/((1)/(2)-1)=8 \end{gathered}`

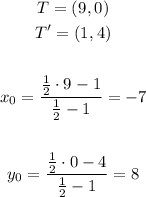
Then, the center of dilatation is

`(-7,8)`