Question

Suppose that there are two types of tickets to a show: advance and same-day. Advance tickets cost $30 and same-day tickets cost $20. For one performance, there were 55 tickets sold in all, and the total amount paid for them was $ 1300. How many tickets of each type were sold?Number of advance tickets sold: Number of same-day tickets sold: Solve by using system of linear equations.

Answer 1

Advance tickets: $30

Same-day tickets: $20

Tickets sold: 55

Total money: $1300

Let us say that a represents the number of advance tickets sold, and s is the number of same-day tickets sold. Then, from the total number of tickets sold:

`a+s=55...(1)`

And for the total income:

`\begin{gathered} 30a+20s=1300 \\ 3a+2s=130...(2) \end{gathered}`

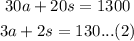
From (1):

`a=55-s...(1^(\prime))`

Using this result on (2):

`\begin{gathered} 3(55-s)+2s=130 \\ 165-3s+2s=130 \\ \Rightarrow s=35 \end{gathered}`

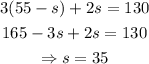
Using this on (1'):

`\begin{gathered} a=55-35 \\ \Rightarrow a=20 \end{gathered}`

Number of advance tickets sold: 20

Number of same-day tickets sold: 35