Question

In the diagram at the right, the endpoints of the chord are thepoints where the line x = 2 intersects the circle x² + y2 = 49.What is the length of the chord?

Answer 1

Given:

The equation of circle is x²+y²=49.

The chord intersects the circle at the line x = 2.

The objective is to find the length of the chord.

The general equation of circle is,

`x^2+y^2=r^2`

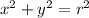
By comparing the general equation with the given equation,

`\begin{gathered} r^2=49 \\ r=\sqrt[]{49} \\ r=7 \end{gathered}`

Consider the given figure as,

Using the right triangle in the circle, the value of x can be calculated using Pythagorean theorem.

`\begin{gathered} AC^2=AB^2+BC^2 \\ 7^2=2^2+x^2 \\ x^2=7^2-2^2 \\ x^2=49-4 \\ x^2=45 \\ x=\sqrt[]{45} \end{gathered}`

Then, the total length of the chord will be,

`\begin{gathered} L=2x \\ =2\sqrt[]{45} \\ =13.4 \end{gathered}`

Hence, the length of the chord is 13.4.