Given:
The equation of circle is x²+y²=49.
The chord intersects the circle at the line x = 2.
The objective is to find the length of the chord.
The general equation of circle is,
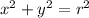
By comparing the general equation with the given equation,
![\begin{gathered} r^2=49 \\ r=\sqrt[]{49} \\ r=7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pzwtoju4i4uhiff6c8jssnw6gwl28w25xa.png)
Consider the given figure as,
Using the right triangle in the circle, the value of x can be calculated using Pythagorean theorem.
![\begin{gathered} AC^2=AB^2+BC^2 \\ 7^2=2^2+x^2 \\ x^2=7^2-2^2 \\ x^2=49-4 \\ x^2=45 \\ x=\sqrt[]{45} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ialkfb0pk6845n72h6pls3untw1jt4cs80.png)
Then, the total length of the chord will be,
![\begin{gathered} L=2x \\ =2\sqrt[]{45} \\ =13.4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yjaggoiwt2pjvzlibae8f14b453j3hxoa5.png)
Hence, the length of the chord is 13.4.