To solve this question we have to set and solve a system of equations.
Let S be the amount (in dollars) that Larry Mitchell invested in the 7% account, and T be the amount (in dollars) that he invested in the 2% account, then we can set the following system of equations:
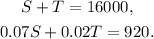
Solving the first equation for T we get:
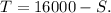
Substituting T=16000-S in the second equation we get:
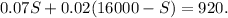
Applying the distributive property we get:

Adding like terms we get:
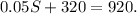
Subtracting 320 from the above equation we get:
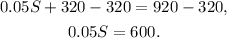
Now, dividing by 0.05 we get:
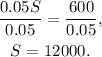
Finally, substituting S=12000 in T=16000-S we get:
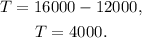
Therefore, Larry invested $12,000 in the 7% account and $4,000 in the 2% account.
Answer: Larry invested $12,000 in the 7% account and $4,000 in the 2% account.