Question

graph two or more functions in the same family for which the parameter being changed is the slope, m, and is less than 0

Answer 1

You need to determine two or more functions that are from the same family as the given one, that is, that these functions should be linear functions.

The parameter you have to change is the slope, and it should be m<0

The given function is.

`f(x)=x+2`

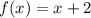
For this function the slope is m=1 and the y-intercept is b=2

Since there are no mo specifications on the charasteristics on the given functions you simply have to change the value of the slope and if you want, the value of the y-intercept.

For example,

A line perpendicular to the given one should have a slope equal to the inverse negative of the original line, that is:

`m_2=-(1)/(m_1)`

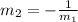
If the slope for the original is m=1, then a perpendicular line would have slope:

`m_2=-(1)/(1)=-1`

The slope is less than zero so it applies.

Now using the point slope form and any point you want this line to cross you can determine the equation for the function:

Lets say the line crosses the point (-2,4)

`\begin{gathered} y-y_1=m(x-x_1) \\ y-4=-1(x-(-2)) \\ y-4=-x-2 \\ y=-x-2+4 \\ y=-x+2 \end{gathered}`

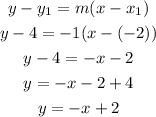
A line of the same family as the given one with slope less than zero is y=-x+6

For the next function you can choose any slope less than one and any point in the coordinate system and using the point slope form, calculate its equation, for example:

m=1/3

Point (4,-4)

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-4)=(1)/(3)(x-4) \\ y+4=(1)/(3)x-(4)/(3) \\ y=(1)/(3)x-(4)/(3)-4 \\ y=(1)/(3)x-(16)/(3) \end{gathered}`

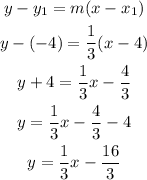
Next is to plot both equations.

For the first one we know its y-intercept (0,2) and the point used to determine the equation (-2,4)

For the second one we know the y-intercept (0,-16/3) and the point used to determine it (4,-4)

With these two coordinates you can plot the lines.