Question

2x+3y-4z=-3-x-2y+3z=4x-z=4solve by substitution

Answer 1

`\begin{gathered} 2x+3y-4z=-3 \\ -x-2y+3z=4 \\ x-z=4 \end{gathered}`

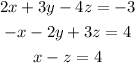
To solve by the equation system by substitution, first, write the third equation for one of the variables, for example, write it for x:

`\begin{gathered} x-z=4 \\ x-z+z=4+z \\ x=4+z \end{gathered}`

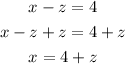
Replace the expression obtained in x in the first equation:

`\begin{gathered} 2x+3y-4z=-3 \\ 2(4+z)+3y-4z=-3 \\ 2\cdot4+2\cdot z+3y-4z=-3 \\ 6+2z+3y-4z=-3 \\ 6+2z-4z+3y=-3 \\ 6-2z+3y=-3 \end{gathered}`

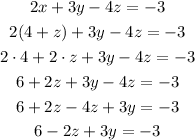
Write the equation for y:

`\begin{gathered} 6-2z+3y=-3 \\ 6-6-2z+3y=-3-6 \\ -2z+3y=-9 \\ -2z+2z+3y=-9+2z \\ 3y=-9+2z \\ (3y)/(3)=-(9)/(3)+(2z)/(3) \\ y=-3+(2)/(3)z \end{gathered}`

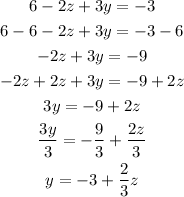
Use the expressions obtained for x and y in the second equation:

`\begin{gathered} -x-2y+3z=4 \\ -(4+z)-2(-3+(2)/(3)z)+3z=4 \end{gathered}`

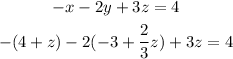
From this expression, you can calculate the value of z:

`\begin{gathered} -4-z-\cdot2(-3)+(-2)((2)/(3)z)+3z=4 \\ -4-z+6-(4)/(3)z+3z=4 \\ -z-(4)/(3)z+3z-4+6=4 \\ (2)/(3)z+2=4 \\ (2)/(3)z+2-2=4-2 \\ (2)/(3)z=2 \\ ((2)/(3)\cdot(3)/(2))z=2\cdot(3)/(2) \\ z=3 \end{gathered}`

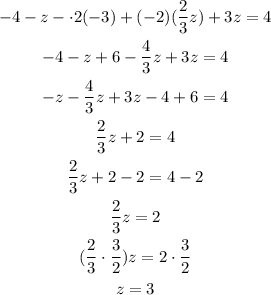
Using the value of z you can calculate the values of y and x

Start with y:

`\begin{gathered} y=-3+(2)/(3)z \\ y=-3+(2)/(3)\cdot3 \\ y=-3+2 \\ y=-1 \end{gathered}`

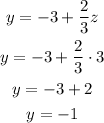
Next, calculate the value of x:

`\begin{gathered} x=4+z \\ x=4+3 \\ x=7 \end{gathered}`

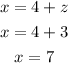
The solution of the equation system is x=7, y=-1 and z=3