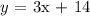We are required to find the line that has the following properties:
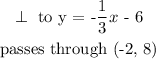
By definition, when two lines are perpendicular, the multiplication of their slopes gives -1 :
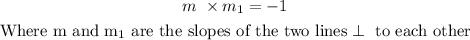
From here, we can find the slope of the line.
let the slope of the line be x
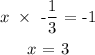
The slope-intercept form of the equation of the line is:
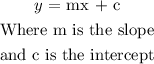
But the slope is 3:
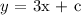
To find the intercept(c), we substitute the point (-2,8) and solve for c:
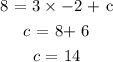
Hence, the equation of the line is: