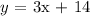Question

I need help with this problemfind the slope of the line

Answer 1

We are required to find the line that has the following properties:

`\begin{gathered} \perp\text{ to y = -}(1)/(3)x\text{ - 6} \\ \text{passes through (-2, 8)} \end{gathered}`

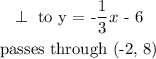
By definition, when two lines are perpendicular, the multiplication of their slopes gives -1 :

`\begin{gathered} m\text{ }* m_1=-1^{} \\ \text{Where m and m}_1\text{ are the slopes of the two lines}\perp\text{ to each other} \end{gathered}`

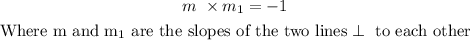
From here, we can find the slope of the line.

let the slope of the line be x

`\begin{gathered} x\text{ }*\text{ -}(1)/(3)\text{ = -1} \\ x\text{ = 3} \end{gathered}`

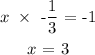
The slope-intercept form of the equation of the line is:

`\begin{gathered} y\text{ = mx + c} \\ \text{Where m is the slope} \\ \text{and c is the intercept} \end{gathered}`

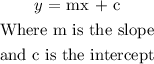
But the slope is 3:

`y\text{ = 3x + c}`

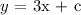
To find the intercept(c), we substitute the point (-2,8) and solve for c:

`\begin{gathered} 8\text{ = 3}*-2\text{ + c} \\ c\text{ = 8+ 6} \\ c\text{ = 14} \end{gathered}`

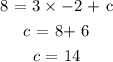
Hence, the equation of the line is:

`y\text{ = 3x + 14}`